こんにちは、蒼い小鳥です
薬剤師になって数年経ち、今は管理薬剤師をやっています
薬学実習生に教えることも多く、理解していないように感じています
薬学実習生がどんなに一問一答形式で覚えてもそれだけでは武器にならず、少し違う視点からの問題になってしまうとほとんど回答できないようです
私がやってきた勉強方法ではそのような問題が出てしまっても解けると思います
少しでも参考になれば嬉しいです!
今回は物理、物理薬剤のどちらにも出てくる反応速度論にある反応次数と反応速度定数についてやっていきましょう
反応速度とは

物理でよく問われる反応速度とは、時間当たりの濃度変化のことを言う
濃度変化は、反応物の濃度減少や生成物の増加などで表されています
よく使われる式として
\(反応速度v=\frac{濃度変化}{反応時間}=±\frac{dC}{dt}\)
C:反応物または生成物(分解物)の濃度
±の理由は濃度の増減によって変わります
- 濃度が増える時は、速度が\(\frac{dC}{dt}\)
- 濃度が減る時は、速度が\(-\frac{dC}{dt}\)
とありますが、この反応速度の式で私が覚えてほしいと思っている式はこれです!
\(-\frac{dC}{dt}=k・C ^ n\)
k:反応速度定数 n:反応次数 C:反応物の濃度(残存濃度)
反応次数と計算については反応次数で解説
反応速度定数(分解速度定数)とは

反応速度定数kは、反応のしやすさを表している値
反応速度定数は温度やpHなどの影響を受けてしまう!
薬の分解を考えると分解されやすいかされづらいかを考えると安定しているか不安定かが見えてくる
- 反応速度定数が大きいと分解しやすくため、壊れやすい不安定な薬剤
- 反応速度定数が小さいと分解しづらくため、壊れにくい安定な薬剤
反応次数の分類について

反応次数には先ほど説明した式を使う
\(-\frac{dC}{dt}=k・C ^ n\)
k:反応速度定数 n:反応次数 C:反応物の濃度(残存濃度)
問題では基本的にnには0.1.2のどれかが入ります
n=0の場合は0次反応、n=1の場合は1次反応、n=2の場合は2次反応となります
では、0~2次反応について考えていきましょう!
0次反応とは
0次反応は\(-\frac{dC}{dt}=k・C ^ n\)の式のnに0を入れるのでC0=1となり
\(-\frac{dC}{dt}=k\)
となります
この式より、反応速度定数は濃度に無関係に一定であることが分かります(濃度がなくなるので)
また、この反応を縦軸を残存濃度、横軸を時間に表すと
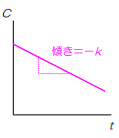
このようになり、初濃度はC₀ 傾きは-k 時間はtで表すと以下のような式になります
このグラフから初めの濃度から一定速度で濃度が減ることをイメージで覚えてください
そして、0次反応で重要な式がこれです
\(C=C₀-kt\)
となります
そして、この濃度が半減期(濃度が半分になる時間)t1/2を求めたいので
\(C=C₀-kt\)にt=t1/2と\(C = \frac{C₀}{2}\)を代入すると
\(\frac {C₀} {2}=C₀-kt1/2\) 右辺と左辺の値を移動
\(kt1/2=C₀-\frac{C₀}{2}\)
\(kt1/2=\frac{C₀}{2}\)
\(t1/2=\frac{C₀}{2k}\)
となり、半減期は初濃度に比例関係であることが分かります
\(t1/2=\frac{C₀}{2k}\)
最後に、0次反応のkの次元についても少しだけ説明
先ほど求めた\(t1/2=\frac{C₀}{2k}\)を式変換して
\(k=\frac{C₀}{2t1/2}\)
\(k=\frac{C₀}{2t1/2}\)
この式変換より\(反応速度定数k=\frac{濃度}{時間}\)になっているので次元は濃度x時間-1だと分かります
1時反応とは
1次反応は\(-\frac{dC}{dt}=k・C ^ n\)の式のn=1を入れるので
\(-\frac{dC}{dt}=k・C\)
となります
この式より、反応速度定数は濃度に比例関係であることが分かります
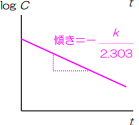
また、この反応を縦軸を残存濃度、横軸を時間に表すと
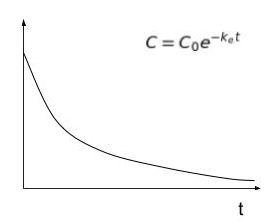
このようになります
ですがこの式にあるeはどこから来たのかを考えてしまうと時間を大幅に使ってしまいます
そのため、次のグラフで覚えるようにしてください
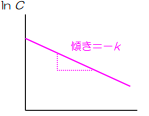
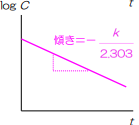
また、1次式反応も0次と同じで右肩下がりの一直線のグラフができると覚えてください
そして、1次反応で重要な式はこれです
\(lnC=lnC₀-kt\)
上の式を覚えることで、常用対数(log)に変換しやすくなります
(自然対数(ln)から常用対数(log)への変換はまとめの最後に記載しますので良ければ時間があるときに見てください)
常用対数に返還後はこの式です
\(logC=logC₀-\frac{k}{2.303}t\)
そして、この濃度の半減期(濃度が半分になる時間)t1/2を求めたいので
\(lnC=lnC₀-kt\)に\(t=t1/2\)と\(C=\frac{C₀}{2}\)を代入すると
\(ln\frac{C₀}{2} = lnC₀-kt1/2\)
\(lnC₀-ln2 = lnC₀-kt1/2\) 右辺と左辺の値を移動
\(kt1/2 = lnC₀-lnC₀+ln2\)
\(kt1/2 = ln2\)
となり、半減期は初濃度に無関係であることが分かります
\(t1/2=\frac{ln2}{k}=\frac{0.693}{k}\)
\(ln2=0.693\)であるため
最後に、1次反応のkの次元についても少しだけ説明
先ほど求めた\(t1/2=\frac{ln2}{k}\)を式変換して
\(k=\frac{ln2}{t1/2}\)
この式変換より\(反応速度定数k=\frac{}{時間}\)になっているので次元は時間-1だと分かります
2次反応とは
2次反応は\(-\frac{dC}{dt}=k・C ^ n\)の式のnに2を入れるので
\(-\frac{dC}{dt}=k・C ^ 2\)
となります
この式より、反応速度定数は濃度の2乗に比例であることが分かります
また、この反応を縦軸を残存濃度の逆数、横軸を時間に表すと
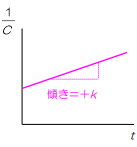
このように右肩上がりの一直線のグラフができると覚えてください
そして、2次反応の式はこれです
\(\frac{1}{C}=\frac{1}{C₀}+kt\)
となります
そして、この濃度の半減期(濃度が半分になる時間)t1/2を求めたいので
\(\frac{1}{C}=\frac{1}{C₀}+kt\)に\(t=t1/2\)と\(C=\frac{C₀}{2}\)を代入すると
\(\frac{1}{C₀/2}=\frac{1}{C₀}+kt1/2\) \(\frac{1}{C₀/2}\)をわかりやすいよう変換
\(\frac{2}{C₀}=\frac{1}{C₀}+kt1/2\)
\(\frac{2}{C₀}=\frac{1}{C₀}+kt1/2\) \(\frac{1}{C₀}\)を左辺へ移動
\(kt1/2=\frac{2}{C₀}-\frac{1}{C₀}\)
\(kt1/2=\frac{1}{C₀}\)
\(t1/2=\frac{1}{kC₀}\)
となり、半減期は初濃度に反比例関係であることが分かります
\(t1/2=\frac{1}{kC₀}\)
最後に、2次反応のkの次元についても少しだけ説明
先ほど求めた\(t1/2=\frac{1}{kC₀}\)を式変換して
\(k=\frac{1}{C₀t1/2}\)
この式変換より\(反応速度定数k=\frac{}{濃度・時間}\)になっているので次元は濃度-1・時間-1だと分かります
まとめ

今回は反応速度論の反応次数と反応速度定数について行いました
0次反応のポイント
- 速度式は\(-\frac{dC}{dt}=k・C ^ n\)
- 特徴は反応速度は濃度と無関係で一定
- 式は\(C=C₀-kt\)
- グラフは右肩下がりのグラフ

- 半減期は\(t1/2=\frac{C₀}{2k}\)
- kの次元は速度・時間-1
1次反応のポイント
- 速度式は\(-\frac{dC}{dt}=k・C\)
- 特徴は反応速度定数は濃度に比例関係
- 式は\(lnC=lnC₀-kt\)もしくは\(logC=logC₀-\frac{k}{2.303}t\)
- グラフは右肩下がりのグラフ

- 半減期は\(t1/2=\frac{ln2}{2}=\frac{0.693}{2}\)
- kの次元は時間-1
2次反応のポイント
- 速度式は\(-\frac{dC}{dt}=k・C ^ 2\)
- 特徴は反応速度定数は濃度の2乗に比例関係
- 式は\(\frac{1}{C}=\frac{1}{C₀}+kt\)
- グラフは右肩上がりのグラフ

- 半減期は\(t1/2=\frac{1}{kC₀}\)
- kの次元は速度-1・時間-1
今回もこれにて以上です
閲覧いただきありがとうございました
自然対数から常用対数への変換式
\(lnC=lnC₀-kt\) 分かりやすく変換
\(logeC=logeC₀-kt\) 対数がついている2つを\(\frac{log10C₀}{log10e}\)の形に変換
\(\frac{log10C}{log10e}=\frac{log10C₀}{log10e}-kt\) 両辺にlog10eをかける
\(log10C=log10C₀-ktlog10e\) \(log10e\)を\(\frac{logee}{loge10}\)の形に変換
\(log10C=log10C₀-kt\frac{logee}{loge10}\) \(logee\)は1なので消せる
\(log10C=log10C₀-\frac{kt}{loge10}\) 見やすく変換と\(loge10=2.303\)を代入
\(log10C=log10C₀-\frac{k}{2.303}t\)
お借りしたグラフが記載されたサイト、PDF




コメント